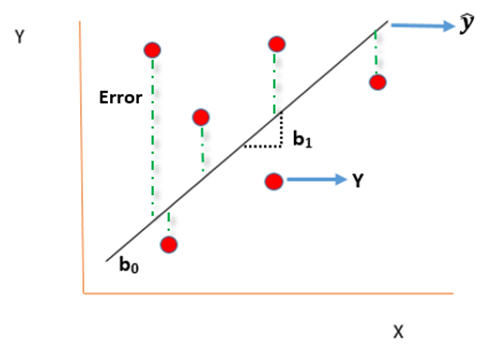
Today’s blog explores another vital statistical concept Linear Regression, let’s begin. Linear regression is normally used in statistics for predictive modeling. It tries to model a relationship between two independent (explanatory variable) and dependent (explained variable) variables X and Y by fitting a linear equation (Y=bo+b1X+Ui) to an observed data.
Assumptions of linear regression
- Ui is a random real variable, where Ui is the difference between the observed dependent variable Y and predicted Y variable.
- The mean of Ui in any particular period is zero.
- The variance of Ui is constant in each period i.e for all values of X, Ui will show the same dispersion around their mean
- The variable Ui has a normal distribution i.e the value of Ui (for each Xi) have a bell shaped symmetrical distribution about their zero mean.
- The random terms of different observations are independent i.e the covariance of any Ui with any other Uj is equal to zero.
- Ui is independent of the explanatory variable X.
- Xi are a set of fixed values in the hypothesised process of repeated sampling which underlies the linear regression model.
- In case there are more than one explanatory variables then they are not perfectly linearly correlated.
Linear Regression equation can be written as:
Where,
is the dependent variable
X is the independent variable.
b0 is the intercept (where the line crosses the vertical y-axis)
b1 is the slope
Ui is the error term (difference between ) also called residual or white noise.

Simple linear regression follows the properties of Ordinary Least Square (OLS) which are as follows:-
- Unbiased estimator:- E()=b ie. an estimator is unbiased if its bias is 0; E() – b = 0
- Minimum Variance:- An estimate is best when it has the smallest variance as compared to any other estimate obtained from other econometric method.
- Efficient estimator:- When it has both the previous properties ie.
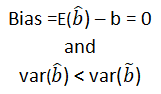
- Linear estimator
- Best, Linear, Unbiased estimator (BLUE)
- Minimum mean squared error (MSE) estimator:- It is a combination of the unbiasedness and minimum variance properties. An estimator is a minimum MSE estimator if it has the smallest mean square error.
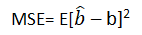
With that the discussion on Linear Regression wraps up here, hopefully it cleared away any confusion you might have and helped you get a grasp on the concept. We have a video discussion on this same topic, which is attached below this blog, check it out for further reference.
Continue to track the DexLab Analytics blog to find informative posts related to Python for data science training.
.
Comments are closed here.